Rumus Online: Matriks

Matriks adalah suatu kumpulan besaran (variabel dan konstanta) yang dapat dirujuk melalui indeknya, yang menyatakan posisinya dalam representasi umum yang digunakan, yaitu sebuah tabel persegipanjang. Matriks merupakan suatu cara visualisasi variabel yang merupakan kumpulan dari angka-angka atau variabel lain, misalnya vektor. Dengan representasi matriks, perhitungan dapat dilakukan dengan lebih terstruktur. Pemanfaatannya misalnya dalam menjelaskan persamaan linier, transformasi koordinat, dan lainnya. Matriks seperti halnya variabel biasa dapat dimanipulasi, seperti dikalikan, dijumlah, dikurangkan dan didekomposisikan.

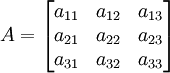$A =\begin{bmatrix}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33} \\\end{bmatrix}\!$

Penjumlahan dan pengurangan matriks

Penjumlahan dan pengurangan matriks dapat dilakukan dengan mengoperasikan komponen matriks pada letak yang sama, atau dilambangkan dengan

$a_{ij} \pm b_{ij} = c_{ij}\!$

atau dalam representasi dekoratfinya

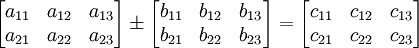
$\begin{bmatrix}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\\end{bmatrix}\pm\begin{bmatrix}b_{11} & b_{12} & b_{13} \\b_{21} & b_{22} & b_{23} \\\end{bmatrix}=\begin{bmatrix}c_{11} & c_{12} & c_{13} \\c_{21} & c_{22} & c_{23} \\\end{bmatrix}\!$

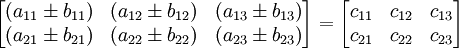
$\begin{bmatrix}(a_{11} \pm b_{11}) & (a_{12} \pm b_{12}) & (a_{13} \pm b_{13}) \\(a_{21} \pm b_{21}) & (a_{22} \pm b_{22}) & (a_{23} \pm b_{23}) \\\end{bmatrix}=\begin{bmatrix}c_{11} & c_{12} & c_{13} \\c_{21} & c_{22} & c_{23} \\\end{bmatrix}\!$

http://id.wikipedia.org/wiki/Matriks_(matematika)

Rumus Online

Matriks

Related Posts :

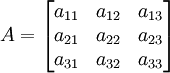
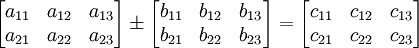
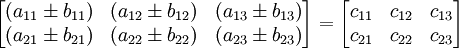
Tidak ada komentar:

Posting Komentar